Math-question-2

Got another question:

Given rectangle ABCD , 2 lines BG and CG intersect at G.

The Area of △ABE=7, △EFG=9, △CDF=9.

Question: Whats the area of Rec ABCD ?

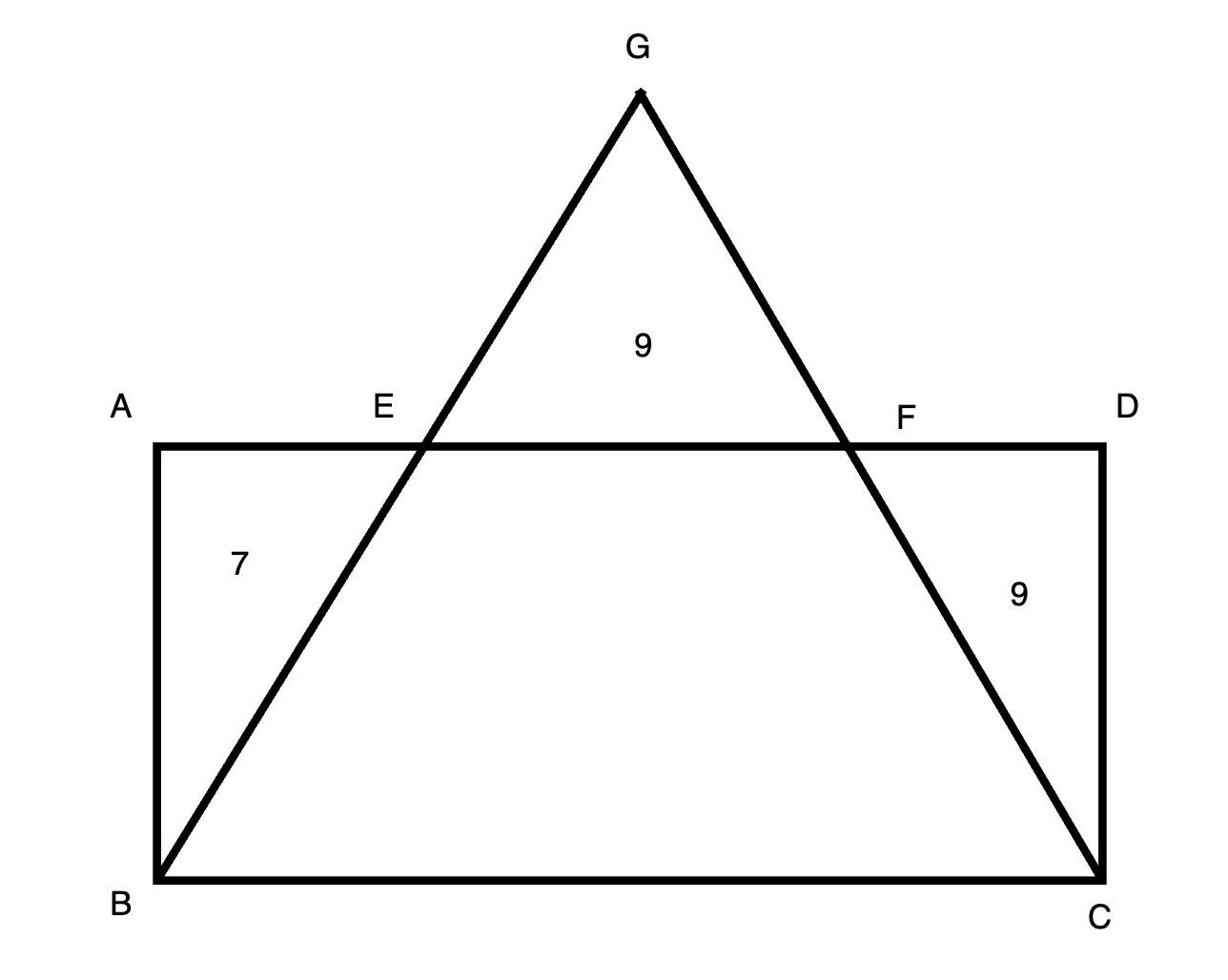
Solve:

Let AB=CD=h, AE=7a, DF=9a. Make GH ⏊ AD at H. Let GH = g:

Because

Let EH = 7b, FH = 9b

Then

△EFG=9 = ==> (a)

And △ABE=7 = $AEAB=(7a)h

So ah = 2 (b)

And for △ABE and △HGE, they are similar, so

So

=>

=> ag = bh (c)

For the given (a), (b), (c),

a*b= And for (c), ag = bh

Then So total S_abcd = 2 * S_abe + 2 * S_CDF + S_EFNM

= 7 * 2 + 9 * 2 + (7b+9b) * h

= 14 + 18+ 16 * b* h

= 32 + 16 *

= 32 + 24

= 56.